И снова здравствуйте, уважаемые одиннадцатиклассники! Полагаю, что Вы хорошо отдохнули и готовы к работе для достижения своих высоких целей.
В этом году июнь месяц выдался очень продуктивным. Моя работа не закончилась 6 июня, когда мои ученики написали ЕГЭ по физике. После публикации результатов ЕГЭ (сначала по математике, а потом и по физике) стало поступать множество сообщений от учеников, даже тех, с кем я не занималась, с просьбой помочь разобраться, за что сняли баллы. А в некоторых случаях даже была необходима помощь с составлением апелляции. Бесценный опыт, если честно…..Только вот от этого опыта седых волос становится больше. И желание сжечь критерии не отпускает меня.
Сразу замечу, что апелляция возможна только по заданиям второй части. По первой части апелляция производится только тогда, когда компьютер неверно считал знак, записанный Вами в бланке ответов.
Уважаемые одиннадцатиклассники, вы должны понимать, что недостаточно просто получить верный ответ, недостаточно записать решение в стиле «я художник, я так вижу». Ваше решение будут оценивать по вполне определенным критериям. И даже абсолютно верный ответ не гарантирует полный балл за выполненное задание.
Анализ ошибок мы начнем с разбора сканов работ по профильной математике. Эти сканы я собирала не один год. К сожалению, в математике, просто за идею решения, за набор формул, не дадут ни одного балла. А снимают баллы за наличие вычислительных ошибок, недостаточную обоснованность, наличие лишних записей. Не указали необходимые признаки, свойства, теоремы – все, полный балл Вам не дадут.
Основной упор будет сделан на задачи 12, 14, 15 (уравнения, неравенства, задачи с экономическим содержанием). Это так называемый джентельменский набор, который старается выполнить большая часть выпускников. Погнали…
Для удобства статья представлена в двух форматах. Текст и видео. Вот ролик:
Уравнения
Основные ошибки:
1) неправильное использование формул приведения.
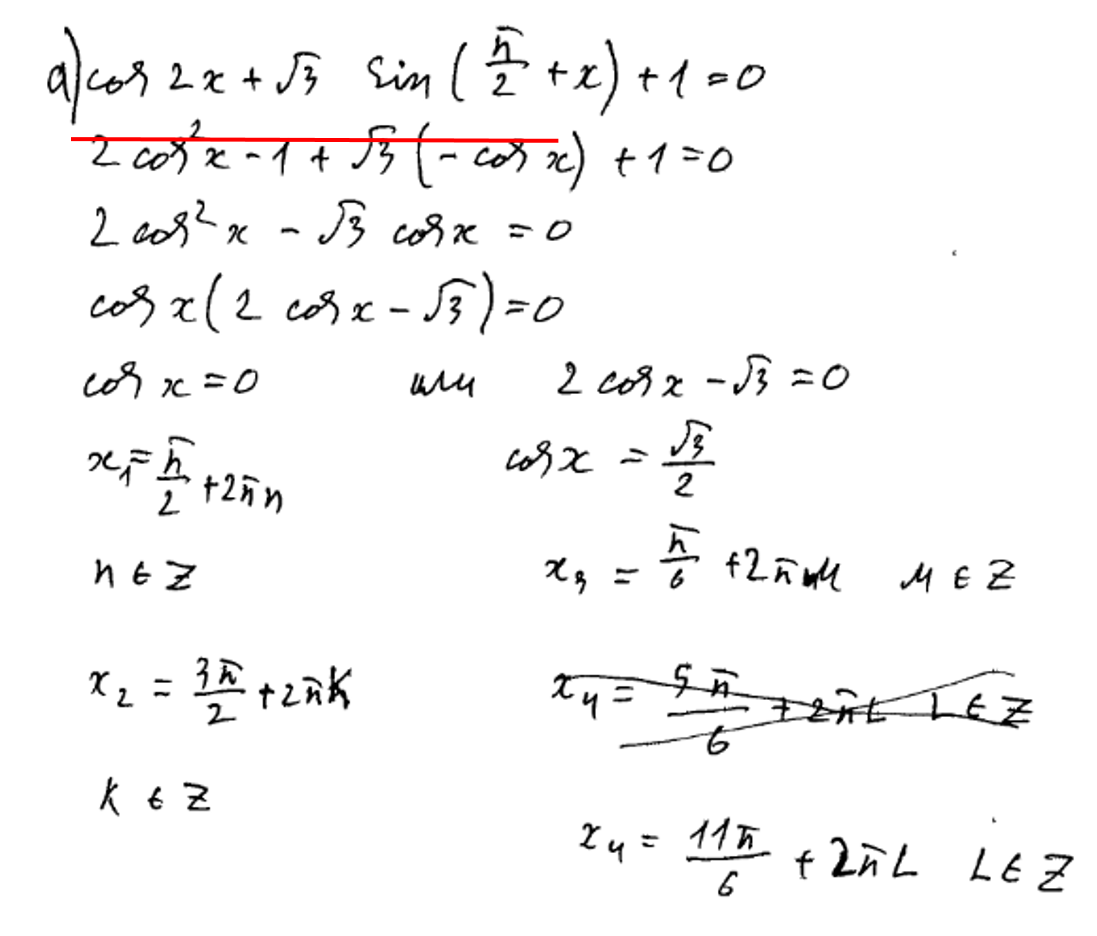
При преобразовании 
допущена ошибка. Минуса перед косинусом быть не должно. Задание оценивается в 0 баллов.
2) незнание свойств четных и нечетных функций. Также ребята забывают, что косинус функция честная, а вот синус, тангенс и котангенс нечетные.
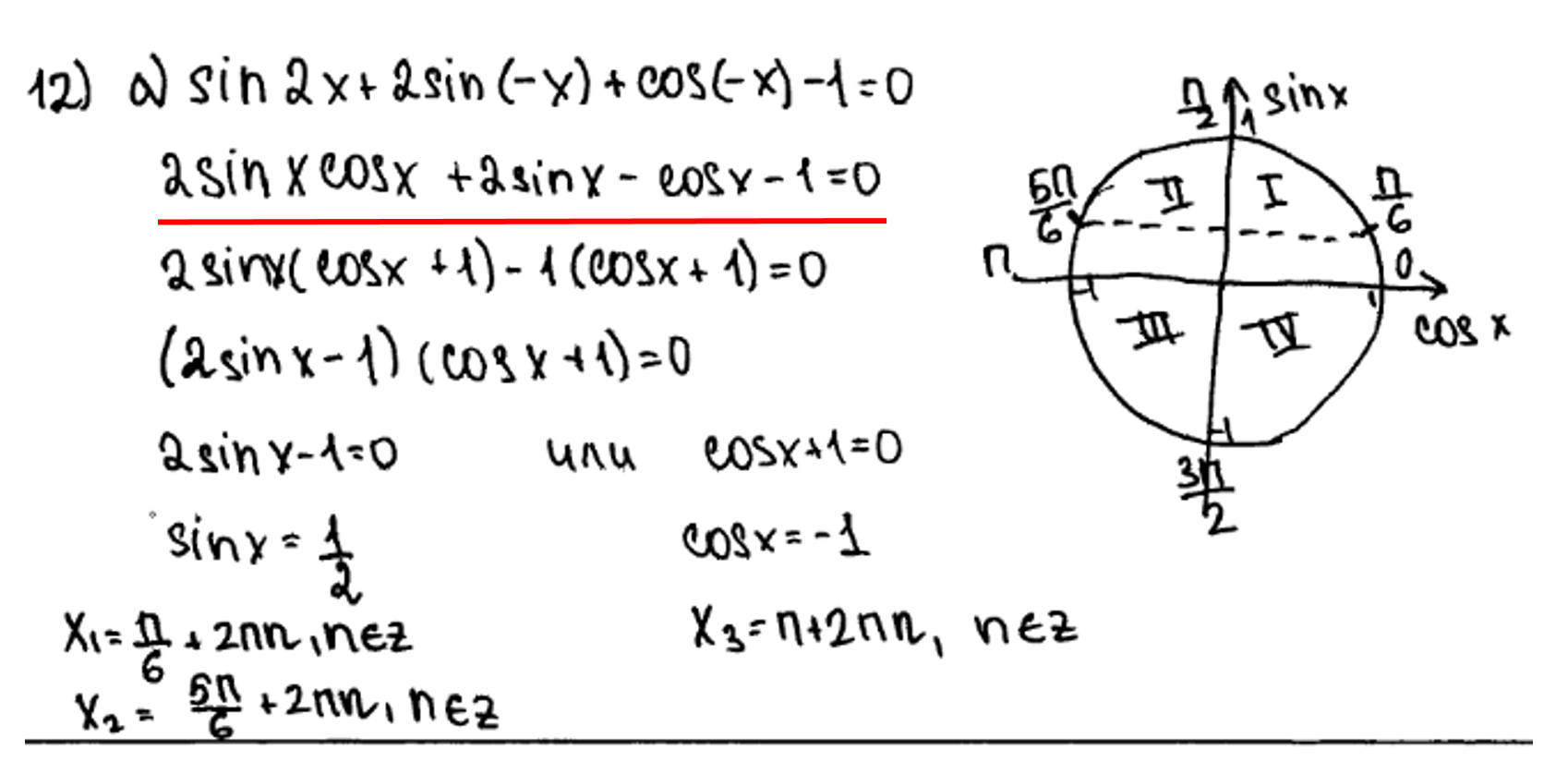
Классическая ошибка! 
– нечетная функция, следовательно знак минус выносится вперед, а не пропадает. Если бы функция была четная, то мы смело могли бы убрать знак минус. Задание оценивается в 0 баллов.
3) неправильное или некорректное использование тригонометрических формул.
Пару лет назад мне написал ученик, которому на экзамене досталось уравнение вида 
.
Скан он мне не отправил, но в процессе обсуждений выяснилось, что в первой скобке для 
он использовал не формулу синуса суммы, а формулы приведения. Чего делать категорически нельзя! Как Вы понимаете, задание оценили в 0 баллов.
4) Самое банальное. Неверное решение простейших тригонометрических уравнений.
При решении простейшего тригонометрического уравнения допущена ошибка. Третий и четвертый корень записаны неверно. Задание оценивается в 0 баллов.
Неравенства
С неравенствами у ребят дела идут посложнее, чем с уравнениями. Тут ваша фантазия разыгрывается по полной. Какие только ошибки не встречались(( Постараюсь выделить основные.
1)Пожалуй, самая распространенная ошибка – ошибка в расстановке знаков на координатной прямой. В идеале, если выпускник умеет определять – перед ним корень четного или нечетного порядка, меняется знак или дублируется.
Нули найдены верно. Но при расстановке знаков на координатной прямой допущена ошибка. Мы видим, что единица – нуль числителя второго порядка, следовательно знак сохраняется, и в крайнем левом интервале должен быть плюс. Эта ошибка уже позволяет эксперту поставить за данное задание 0 баллов.
2)Отбрасывание знаменателя и, как следствие, потеря части корней. В примере, приведенном ниже, выпускник отбросил знаменатель и находил нули только числителя.
Это привело к тому, что на координатной прямой не хватает нулей двух скобок: 
.
Такая грубая ошибка на экзамене не прощается.
Оценка эксперта – 0 баллов.
3) Неравносильный переход от неравенства к системе неравенств.
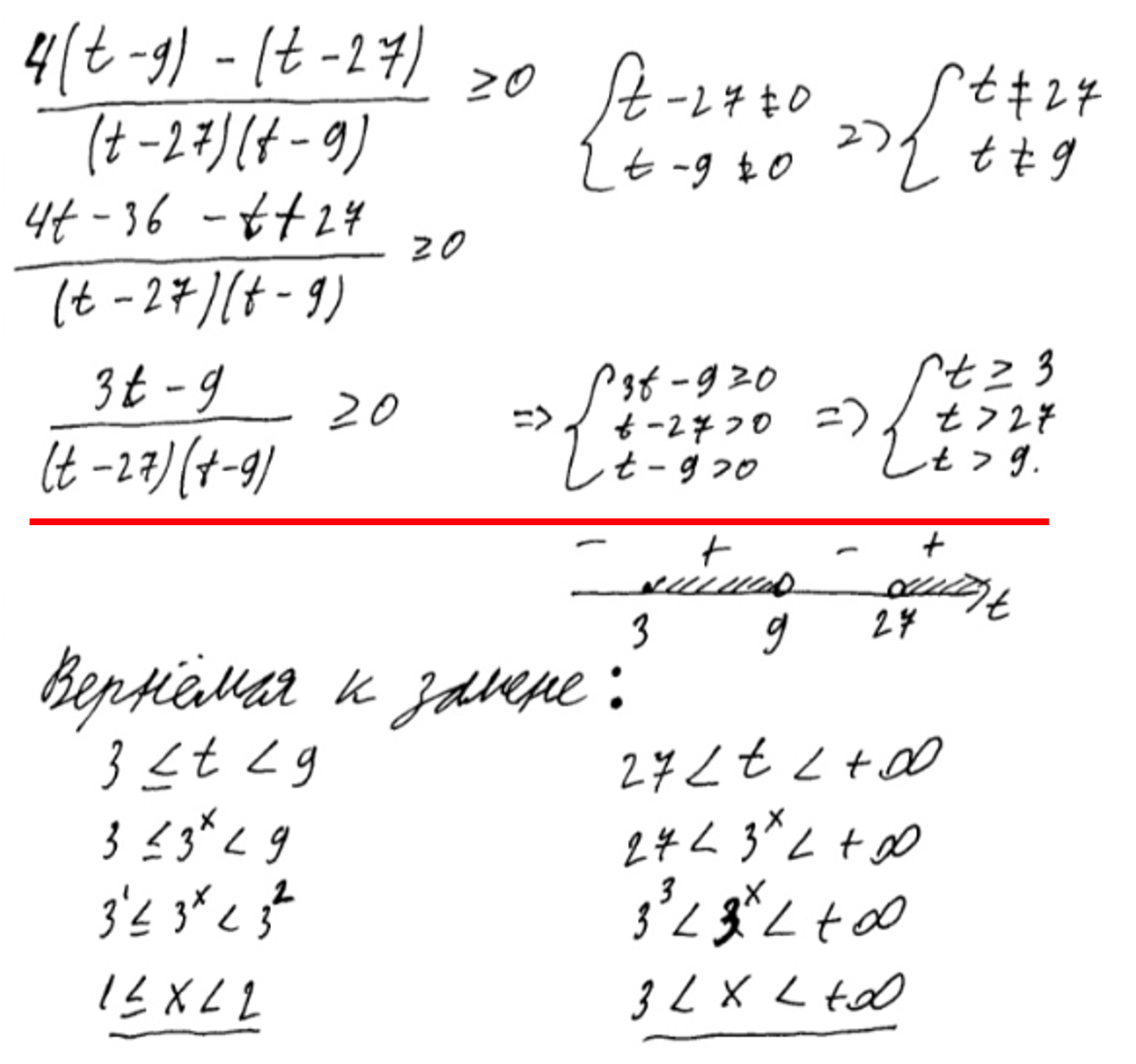
Я думаю, эта ошибка даже не нуждается в комментариях. Даже несмотря на то, что ученик верно нашел нули, верно расставил знаки на координатной прямой, это задание оценили в 0 баллов. Если бы системы с тремя неравенствами не было, ученик имел бы возможность взять полный балл.
4) Ошибки при использовании свойств логарифмов.
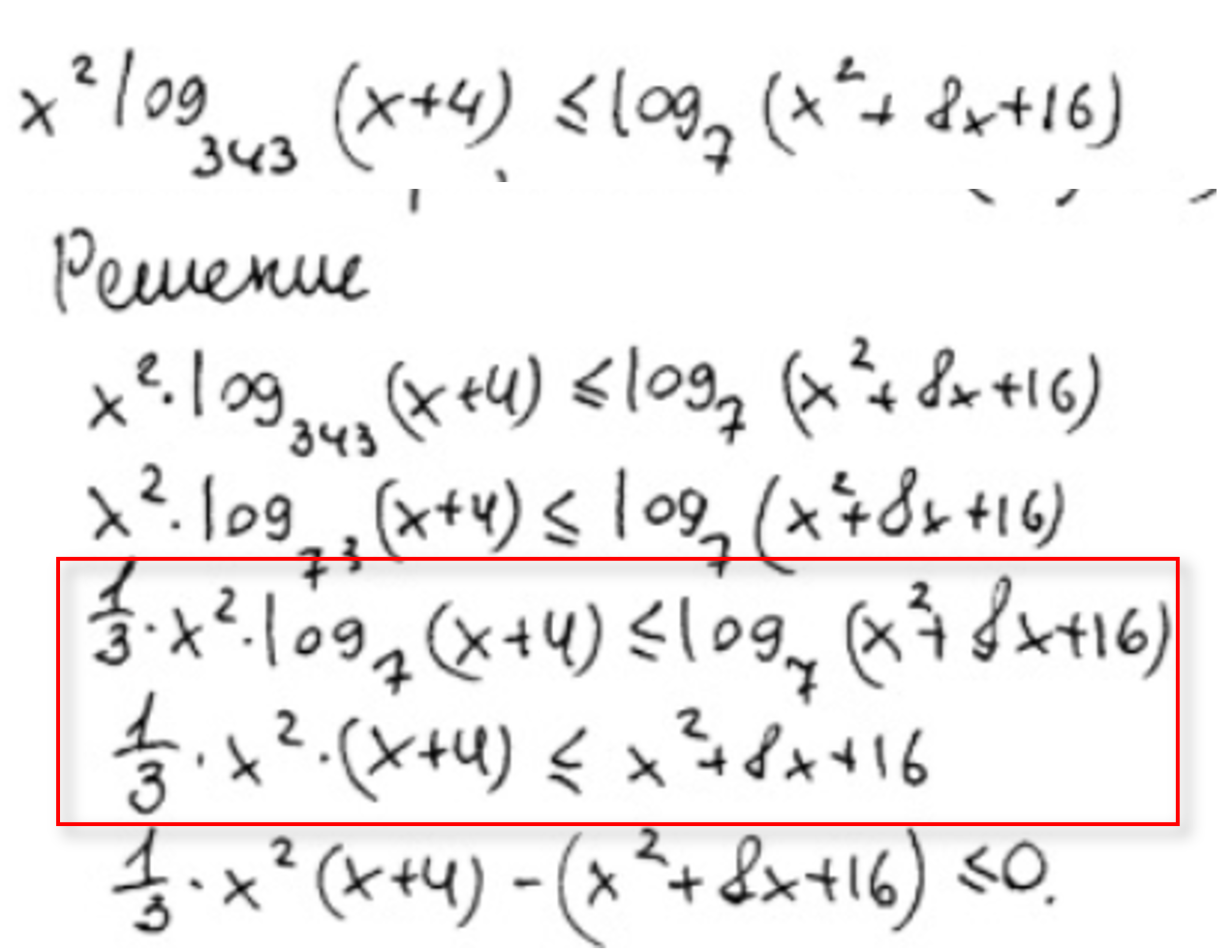
Стоит заметить, что для снятия логарифмов в правой и левой части, необходимо, чтобы перед логарифмом не было никаких цифр или букв. Выпускник снял логарифмы, хотя по задумке нужно было в правой части свернуть в полный квадрат подлогарифмическое выражение и вынести общий множитель. Как Вы понимаете, эксперт оценил это задание в 0 баллов.
Из моего текста у Вас, возможно, сложилось впечатление, что эксперты по всем поводам снимают сразу два балла. К счастью, это не так. Один балл Вам могут поставить, если Вы допустили ошибку в скобке (вместо круглой написали квадратную или наоборот) или допустили вычислительную ошибку, но при этом присутствует верная последовательность всех шагов решения.
Экономические задачи
В решении задач с экономическим содержанием ребятам в первую очередь нужно определить, какая форма кредитования – с дифференцированными платежами, аннуитентными или иная форма кредитования.
Могу выделить несколько основных ошибок.
1)Неверное построение математической модели, связанное с неверным определением формы кредитования.
Для лучшего понимания начну с условия задачи.
В июле 2026 года будет взят кредит на три года в размере 800 тыс рублей. Условия возврата таковы:
– каждый январь долг возрастает на 10 процентов по сравнению с концом прошлого года
– размер платежей в 2027 и 2028 годах одинаковый
– к июлю 2029 года долг выплачивается полностью.
Также известно, что в 2029 году платеж составит 833,8 тыс рублей. Сколько рублей будет составлять платеж в 2027 году?
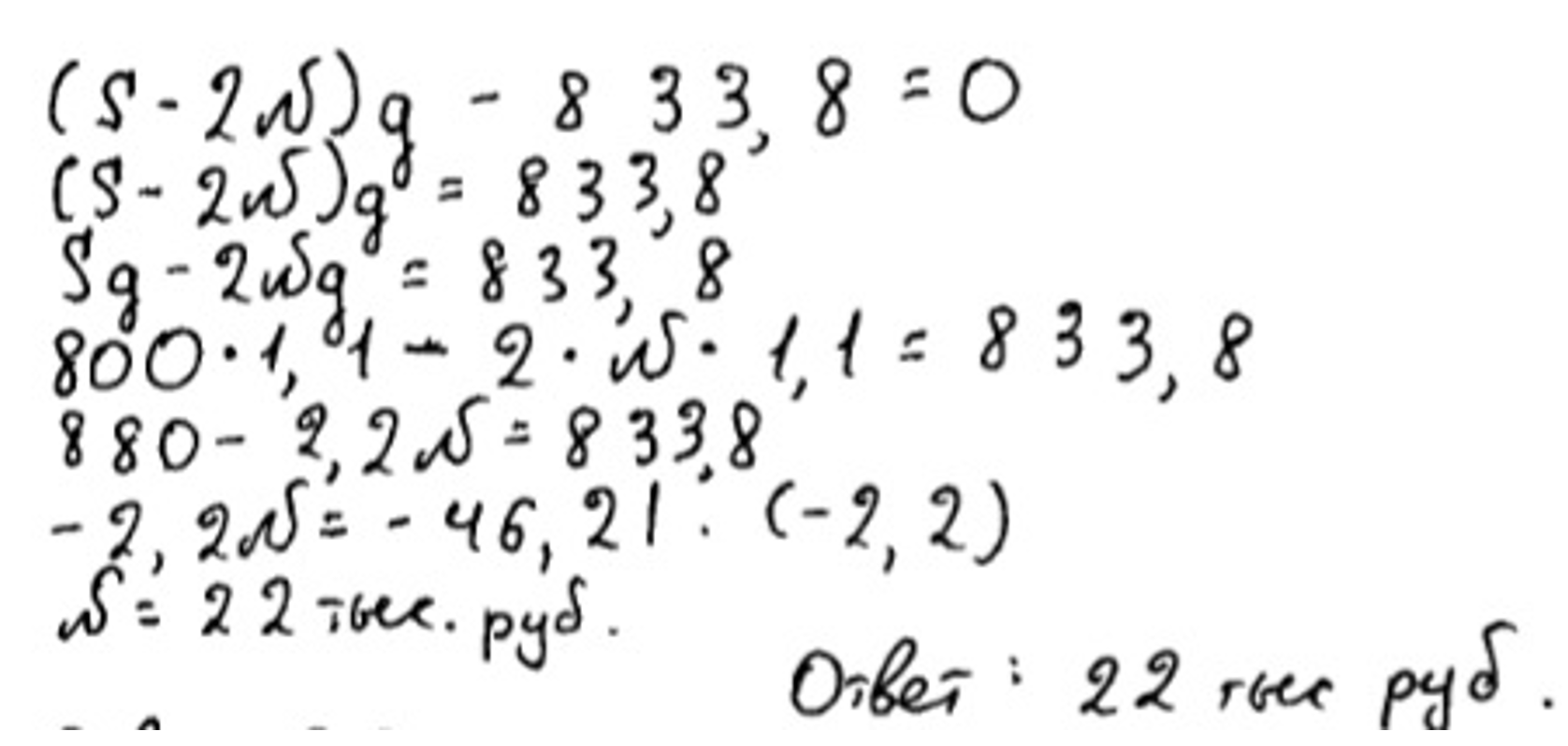
Согласно записям таблицы, ученик решил, что перед ним дифференцированная форма кредитования и остаток уменьшается у него равномерно, ровно на N рублей каждый год. Но это совсем не так. Из условия задачи, мы видим, что выплаты одинаковые первые два года. Но при этом остаток не будет уменьшаться равномерно. Правильная запись остатка во второй строчке должна выглядеть так: 
.
Основываясь на критериях оценивания данного задания, математическая модель построена неверно, задание оценивается в 0 баллов.
Идем дальше. Наверняка Вы встречали задачи вида:
15 января 2020 года был выдан кредит на сумму 900 тыс. рублей на 31 месяц. Условия возврата таковы:
– 1 -го числа каждого месяца долг увеличивается на 2 по сравнению с концом предыдущего месяца.
– со 2 по 14 число необходимо выплатить часть долга;
– 15 -го числа каждого месяца с 1-го по 30-й долг должен быть на одну и ту же величину меньше долго на 15 число предыдущего месяца;
– 15 июля 2027 года долг составит 300 тыс рублей.
– 15 августа 2027 года долг должен быть выплачен полностью.
Найдите общую сумму выплат после полного погашения кредита.
В этой таблице полностью неправильно записаны столбцы с остатками и выплатами. Согласно условию задачи, первые 30 месяцев долг уменьшается равномерно, на 
меньше чем, прошлом месяце. Но не забываем, что первоначальный долг – это S, а не Sk рублей. То есть остаток в первые 30 месяцев должен выглядеть так: 
. Как Вы понимаете, и выплаты будет принимать совсем другой вид, так как они получаются путем вычитания из долга после начисления процентов самого остатка. Для примера запишем первую выплату: 
.
С учетом полностью неправильно построенной математической модели, задание оценивается в 0 баллов.
2)Ошибки при применении формул арифметической прогрессии и расчета общей суммы выплат.
Год назад ребятам на экзамене попалась задача, где в процессе кредитования менялась процентная ставка. Приведу пример:
25 августа 2020 года был дан кредит на 12 лет в размере 300 тыс рублей.
– 25 января с 2021 по 2026 года долг возрастает на 10 процентов;
– 25 января с 2027 по 2032 года долг возрастает на 15 процентов;
– с февраля по июль необходимо выплатить часть долга;
– в августе каждого года долг должен быть на одну и туже величину меньше по сравнению с августом прошлого года;
– к августу 2032 года кредит должен быть полностью погашен.
Найдите общую сумму выплат после полного погашения кредита.
Я уверена, что для многих ребят покажется очевидным, что нельзя складывать первую и последнюю (двенадцатую) выплату. Но я все же поясню.
Действительно, это задача на дифференцированные платежи. И можно заметить, что выплаты подчиняются арифметической прогрессии. Но так как у вас меняется процентная ставка, у Вас меняется и так называемый коэффициент или разность арифметической прогрессии. Поэтому правильно будет сначала просуммировать по формуле арифметической прогрессии первые шесть выплат, потом вторые шесть и полученные выражения сложить. Таким образом Вы получите верный ответ.
В каком же случае Вы можете получить 1 балл – если Вы верно построили математическую модель, но допустили вычислительную ошибку при получении численного значения.
PS: в подавляющем большинстве работ, которые поступали на проверку, ребята просили пояснить, почему за параметр (17 задание) и за задание на числа и их свойства так сильно срезали баллы. В большинстве случаев ребята получали по одному баллу за параметр, а в задаче на числа им засчитывали только пункт а), который также дает только один балл. Ребята, эти задачи считаются олимпиадными, не зря за их полное выполнение дается целых 4 балла. Критерии оценивания данных номеров очень жесткие. Должно быть и максимальное подробное объяснение, и разбор всех случаев и вариантов. В 17 задании это и правильно построенный график (если это необходимо), и рассчитаные все точки, и правильно раскрытый модуль, и расписанные все значения параметра и т.д и т.д.
В погоне за «легкими «баллами ребята даже не трогают планиметрию и стереометрию. А они, напомню, оцениваются в три балла каждый. Даже если Вы испытываете трудности в геометрии, пункт а (доказательство) не пропускайте мимо, как правило он значительно легче пункта б), где нужно найти численное значение той или иной величины. Но по одному первичному баллу за каждый номер Вы спокойно можете получить.
На этом мой краткий обзор подошел к концу. Я желаю удачи и сил всем одиннадцатиклассникам в этом году. Не бойтесь ЕГЭ, настраивайтесь на работу, идите к своей цели. У Вас все получится!
Все, что не убивает, делает нас сильнее!
P.S.: Вот моя группа ВКонтакте, где я выкладываю подобные тексты, ролики и полезности для ЕГЭ по физике и математике: https://vk.com/public185877660 Подписывайтесь!
