Это статья написана в первую очередь для выпускников, которые совсем скоро пойдут на важный и ответственный бой, называемый единым государственным экзаменом. От исхода этого поединка зависит дальнейший вектор развития. Но прошу Вас, не думайте, что от результатов зависит вся ваша жизнь. Экзамен – это лишь рубеж, испытание, которое нужно пройти с высоко поднятой головой.
Я достаточно давно и интенсивно занимаюсь подготовкой абитуриентов к единому государственному экзамену по математике и физике. После экзамена ребята активно делятся впечатлениями, когда приходят результаты – отправляют сканы работ, которые я внимательно изучаю. И я вижу, что из года в год ребята теряют баллы на вполне конкретных заданиях. И чтобы Ваши потери на экзамене на фоне волнения были минимальными, давайте разберем типичные ошибки ученика на ЕГЭ.
1) Уравнения с квадратным корнем
Не забывайте про ограничения!!! Вообще говоря можно наложить ограничения и на подкоренное выражение и на правую часть:
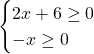
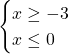
… но если решаете возведением обеих частей в квадрат, то первое неравенство избыточно.
Как альтернатива, выполните проверку, подставив полученные корни в уравнение. Составители очень часто ловят на этом задании, провоцируют указать именно тот корень, который не удовлетворяет ограничениям.
Ограничения актуальны и для обычных дробных уравнений такого вида:
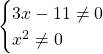
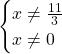
Ну и конечно, куда без ограничений при решении логарифмических уравнений:
Напоминаю, что аргумент логарифма должен быть СТРОГО БОЛЬШЕ НУЛЯ:
Ну а если Вы имеете дело с логарифмом с переменным основанием
то не забудьте, что основание должно быть положительным и не равняться единице.
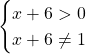
2) Планиметрия
Что касается планиметрии, советую повторить:
1. Формулы для расчета площадей все фигур. Не забудьте повторить, как находится длина дугового сектора и площадь сектора, на всякий случай. Хотя встречаются на ЕГЭ они не так часто.
2. Помните, что медиана в прямоугольном треугольнике не только делит гипотенузу пополам, но и равна половине гипотенузы.
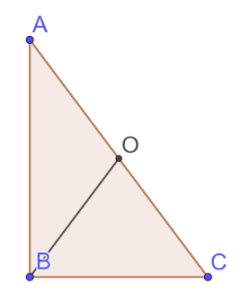
3. Повторите свойства пропорциональных отрезков в прямоугольном треугольнике. Высота, проведенная из вершины прямого угла делит прямоугольный треугольник на два подобных. Расписав отношения сторон всех подобных треугольников Вы придете к формулам:
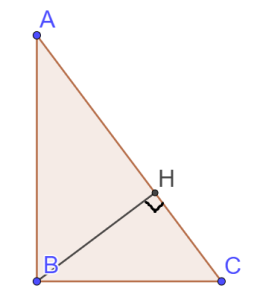
4. Повторите теоремы синусов и косинусов. Теорема синусов бывает весьма полезна для нахождения радиуса описанной окружности
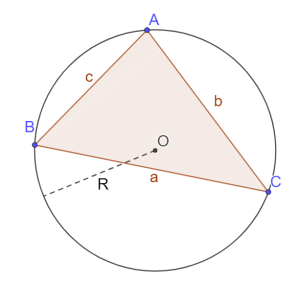
Теорема синусов:
Теорема косинусов:
5. Из года в год найдется ученик, который забудет формулу для расчета радиуса вписанной окружности. А она ведь такая простая!
И работает не только для треугольников, но и для четырехугольников, пятиугольников и так далее. Не забудьте, что в формуле берется ПОЛУПЕРИМЕТР, а S – это площадь фигуры, а не круга!
3) Немного поговорим про преобразование выражений. Чаще всего ребята ошибаются именно в тригонометрии при использовании формул приведения.
Напоминаю алгоритм:
1. Определяем номер четверти, в которой лежит угол.
2. Определяем знак функции. Напоминаю, что знак смотрится по исходной функции.
3. Не забываем, что в точках 
и 
функция меняется на ко-функцию, то есть синус на косинус, косинус на синус, тангенс на котангенс и т.д.
Для лучшего понимания приведу пример
Упростить 
, где 
Шаг 1: Определяем четверть
четв.
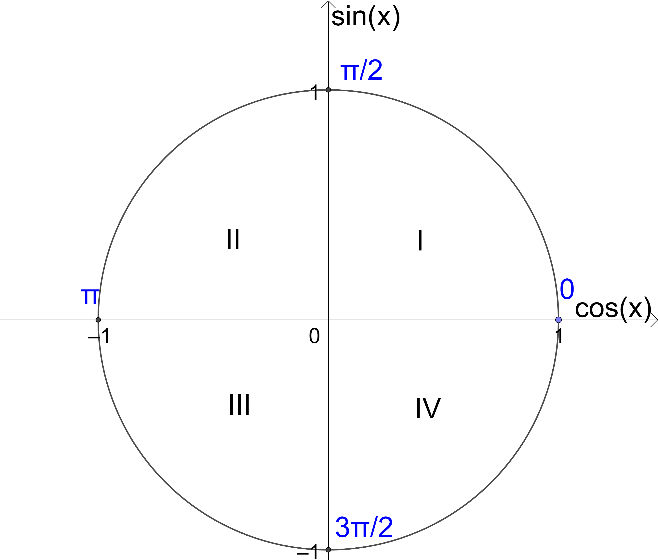
Шаг 2: Определяем знак исходной функции в данной четверти. Знак 
в IV четв. будет отрицательным.
Шаг 3: Так как в выражении есть 
то 
заменим на 
. В итоге получим 
4) Переходим к стереометрии. Тут советы будут аналогичны советам по планиметрии. Повторите все формулы объемов фигур и площадей поверхностей, особенно шара. Легче всего эта формула запоминается, если вы запомните, что площадь поверхности шара – это производная от его объема.
Если Вы имеете дело с комбинацией тел, то внимательно несколько раз прочитайте условие задачи. Цилиндр вписан в призму или описан около призмы, параллелепипед вписан в цилиндр или описан около цилиндра и так далее. Советую держать в голове картинки:
Это – пример призмы, описанной около цилиндра
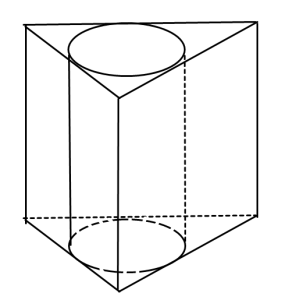
А это – пример призмы, вписанной в цилиндр
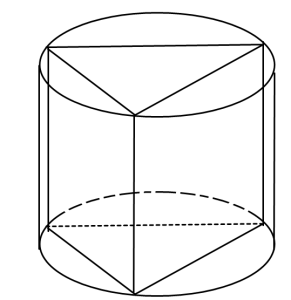
Ну а теперь поговорим о самых распространенных ошибках в стереометрии первой части:
1. Угол между двумя прямыми всегда не более 90 градусов.
Пример:
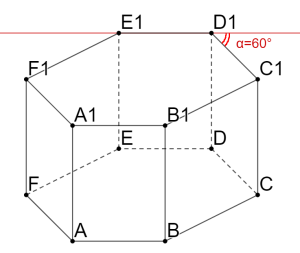
В правильной шестиугольной призме 
, все рёбра которой равны 8, найдите угол между прямыми FA и 
. Ответ дайте в градусах.
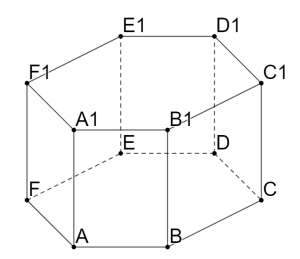
Большая часть ребят проводит прямую 
, параллельную FA и берут угол 
, тем самым получая ответ в 120 градусов. Но это не правильно. Брать нужно смежный угол, который будет равен 60 градусов.
2. Ошибки в применении коэффициента подобия
Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Найдите объем этой призмы, если объём отсеченной призмы равен 20.
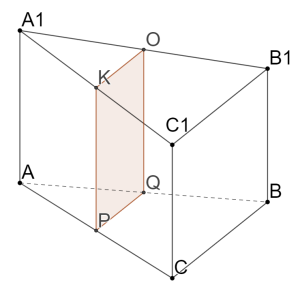
Классический пример – призма и плоскость проведенная через среднюю линию треугольника, лежащего в основании. Ребята полагают, что отношение объемов малой призмы к большой призме равно кубу коэффициента подобия, который в нашем случае равен ½. Но это не так. Отличаются эти призмы только основанием, а вот высоты одинаковы. Следовательно, отношение объемов будет равно отношению площадей оснований. А это квадрат коэффициента подобия.
3. Ошибки в расчете площадей поверхностей составных многогранников.
Классическая проблема в данном случае заключается в том, что ребята достраивают фигуру до куба или параллелепипеда. В этом случае возникает опасность либо посчитать лишнюю поверхность, либо потерять нужную.
Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
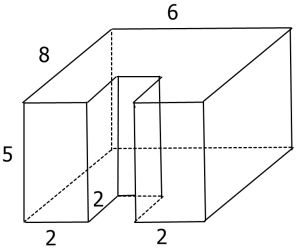
Возможно это немного дольше, но я советую посчитать площадь каждого прямоугольника по отдельности и сложить все значения.
5) График функции и её производной. Наше счастье и наша боль. Мне кажется, эта задача напоминает квест на внимательность. Прежде чем записывать ответ в бланк, советую внимательно несколько раз прочитать задание и для себя ответить на вопрос: я имею дело с графиком функции или ее производной.
1. Если Вы имеете дело с графиком самой функции, то помните, что точки экстремума – это точки, где функция переходит с возрастания на убывание или с убывания на возрастание. Точки пересечения графика с осью х ничего не означают.
Для примера предлагаю рассмотреть следующую функцию:
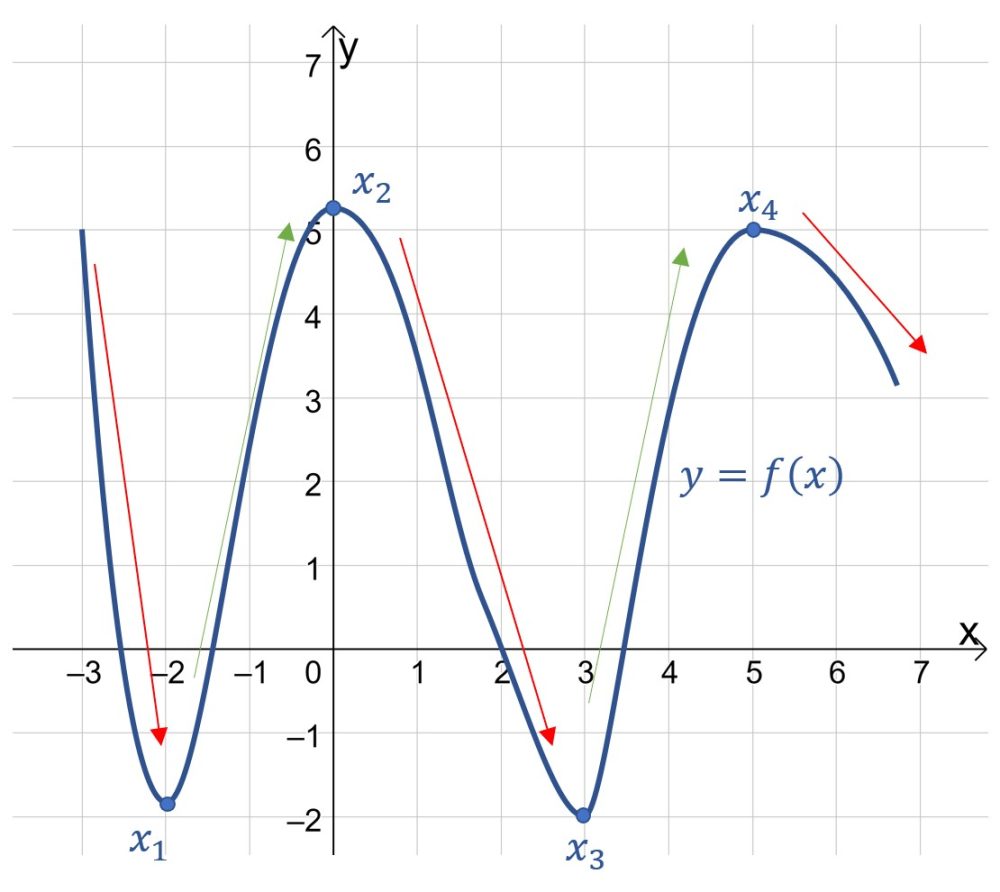
Там, где функция возрастает (зелёные стрелки), производная функции положительна, а там, где функция убывает (красные стрелки), производная функции отрицательная. Производная равна нулю в точках экстремума 
.
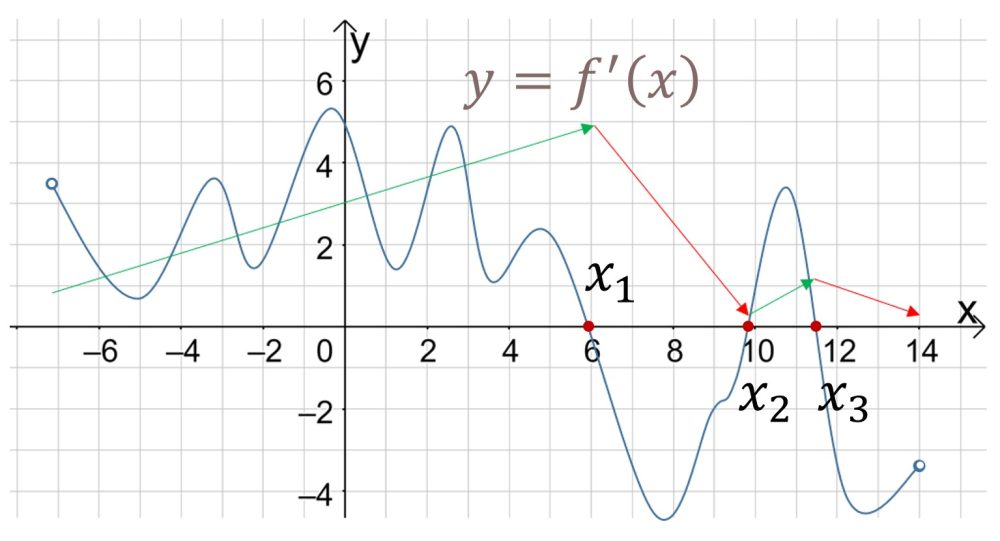
2. Если на экзамене Вам попалась производная функции, то помните: там, где график лежит выше оси х, функция возрастает, там, где график лежит ниже оси х – функция убывает, а точки пересечения графика с осью х-это точки экстремума.
– т. экстремума, 
– т. max, 
– т. min
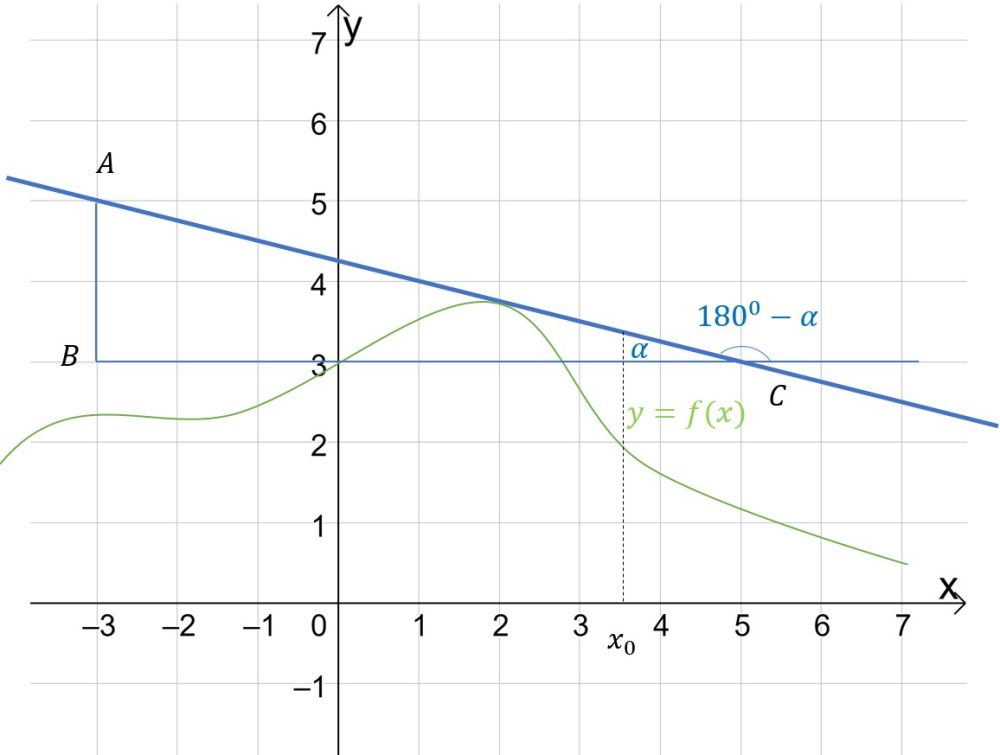
3. Внимательно посмотрите на касательную к графику функции. Если она возрастает, значит значение производной положительно, если убывает-отрицательно.
НЕ ТЕРЯЙТЕ МИНУС В ОТВЕТЕ!
6) Текстовые задачи тоже довольно часто становятся камнем преткновения у выпускников. Советую повторить формулы для суммы арифметической прогрессии, связь концентрации и массы раствора, производительности и работы.
Любимая ошибка выпускников находить среднюю скорость как среднее арифметическое. Не делайте так! Средняя скорость – это общий путь, деленный на общее время.
(Работа = Производительность 
Время)
(Путь = Скорость Время)
Mкислоты=n∙Mраствора
Формула n-го члена арифметической прогрессии:
Сумма первых n членов арифметической прогрессии 
вычисляется по формуле: 
Достаточно тяжело идут у ребят задачи на проценты такого вида:
В 2000 году диван подешевел на 7 процентов, в 2001 подорожал на 8 процентов. Конечная цена 25000 рублей. Найти начальную стоимость.
Советую начальную стоимость обозначить за х, тогда в 2000 году стоимость дивана станет (х-0.07х) =0.93 х рублей, а в 2001 году стоимость будет равна 0.93х*1.08 рублей, которая будет равна 25000 рублей. Можно, конечно, идти с конца, но тогда у ребят возникают сложности, что какую величину обозначить за 100 процентов, что за 107 процентов или может быть за 93 процента.
7) Графики функций. Для правильного выполнения данного номера я советую Вам повторить , какие коэффициенты в функции отвечают за смещение графика вправо или влево, какие вверх или вниз, повторить формулу для расчета вершины параболы 
.
Если у Вас функция вида 
, то коэффициент b отвечает за смещение графика функции вверх или вниз.
А здесь – график с положительным коэффициентом b, равным 2:
Если же Ваш график имеет вид 
, то вы должны понимать, что при положительном значении b ваш график смещается влево, а при отрицательном значении b вправо.
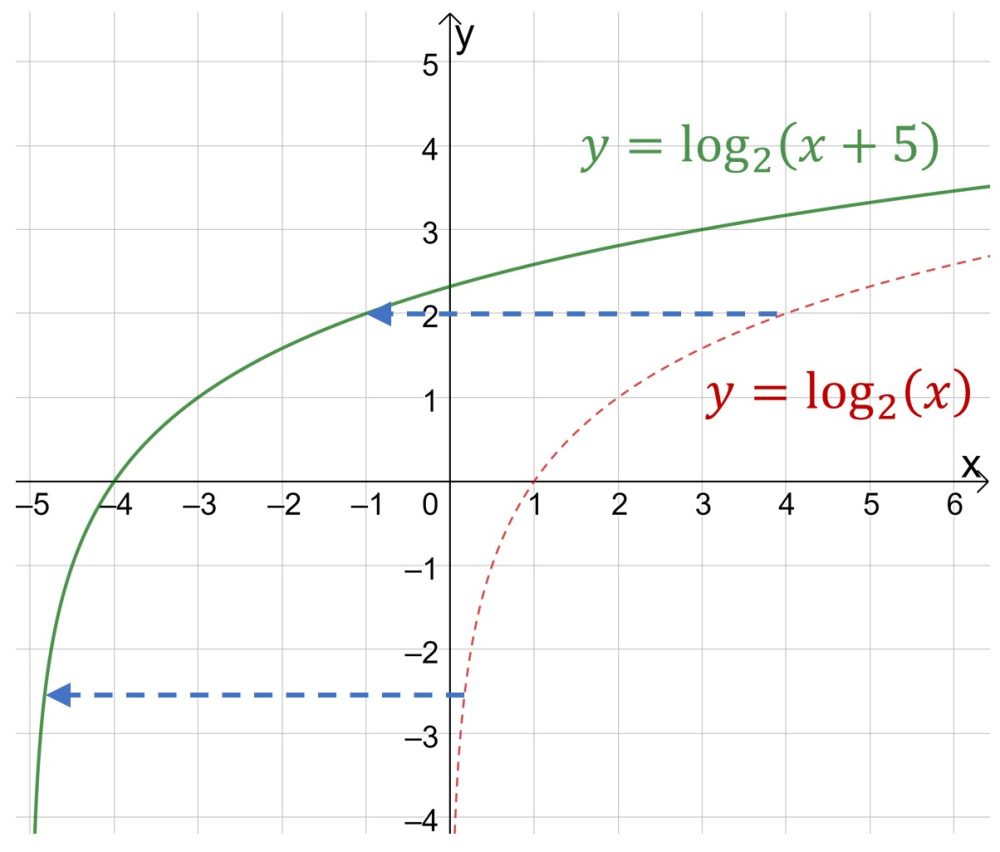
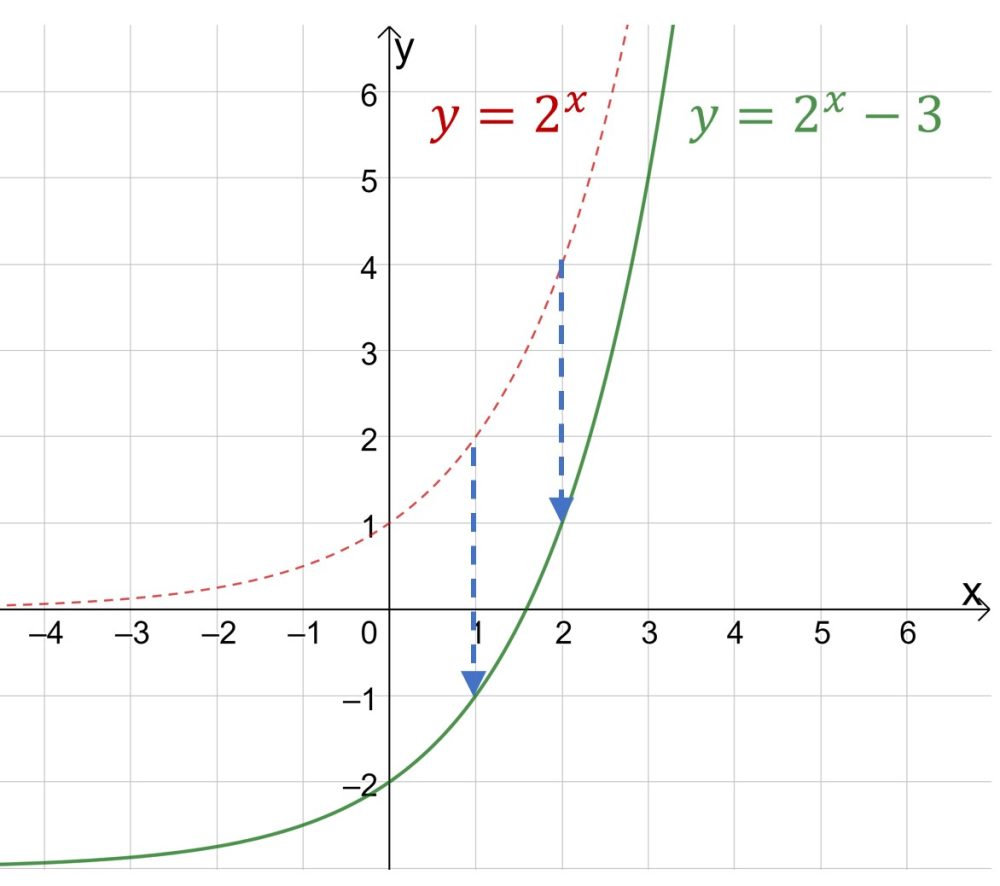
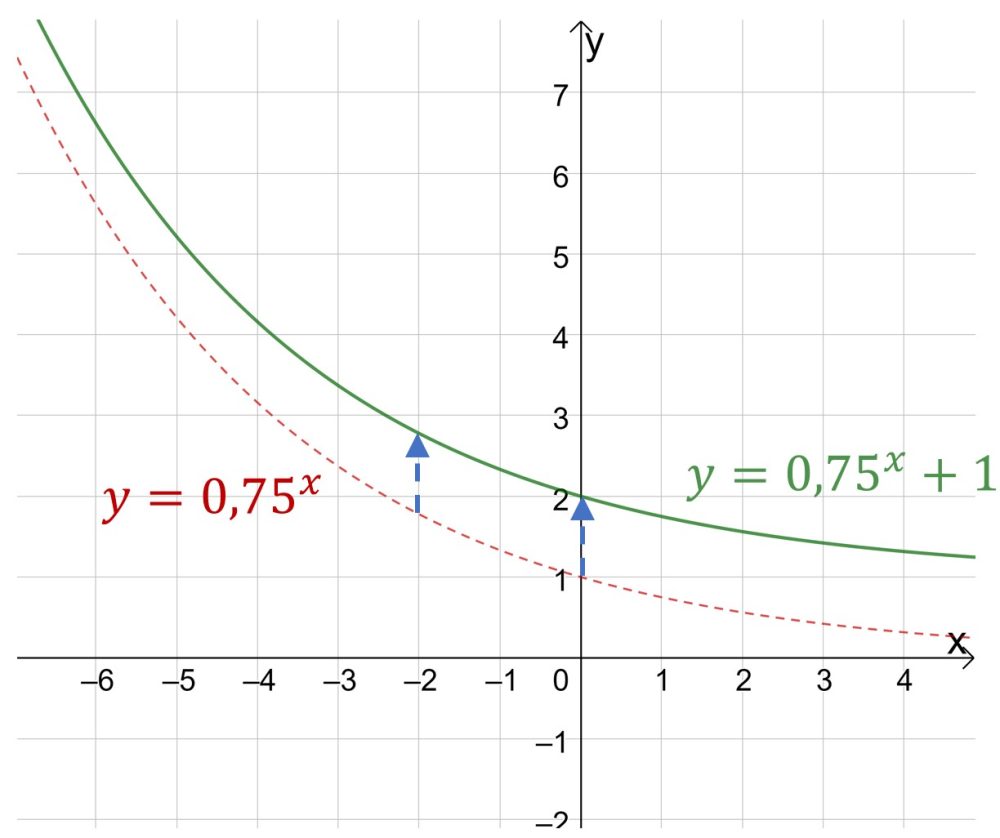
Абсолютно аналогично и с графиками показательной функции.
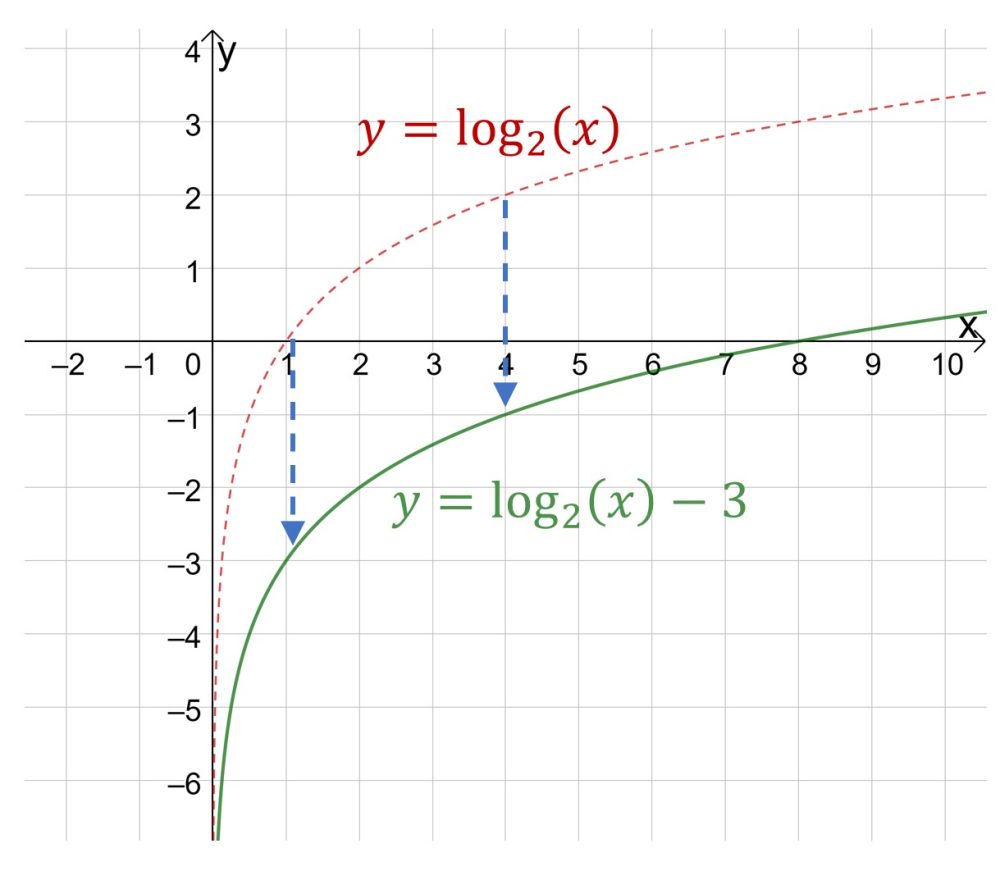
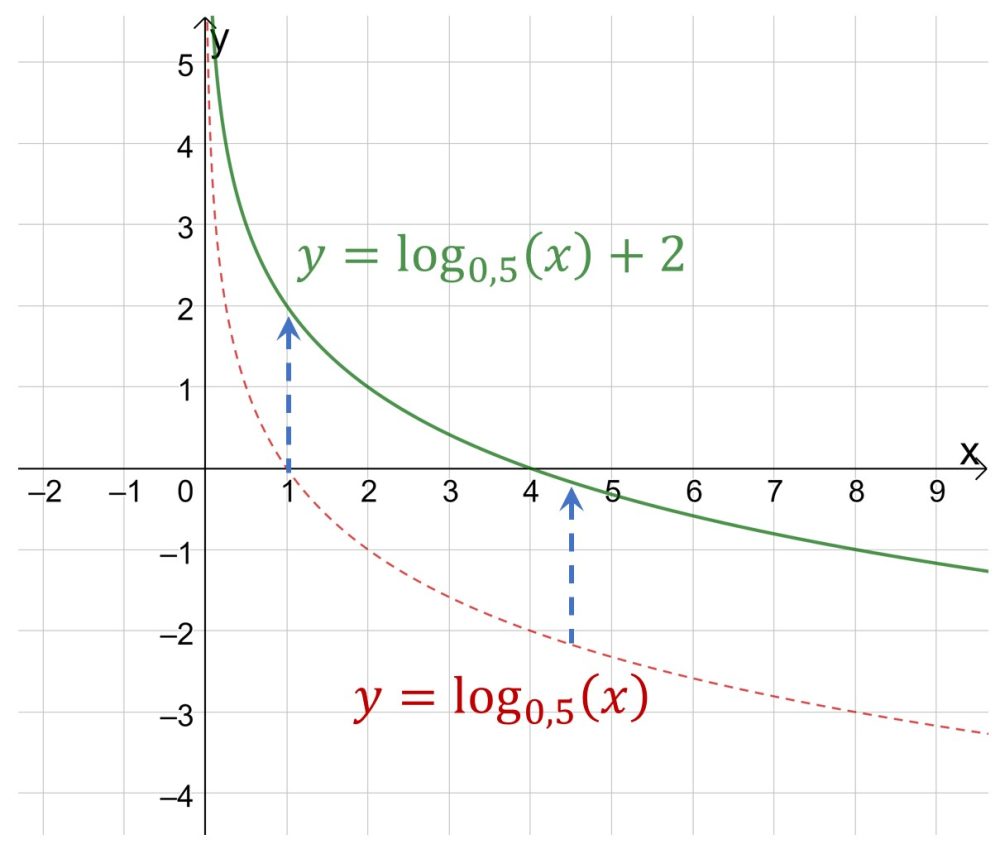
Если вы имеете дело с графиком вида 
, то при положительном b график смещается вверх, при отрицательном b вниз.
На первом графике пример отрицательного коэффициента b, на втором графике пример положительного b.
Ну и не забывайте о графиках показательной функции вида 
. Здесь коэффициент b отвечает за смещение графика функции вправо или влево.
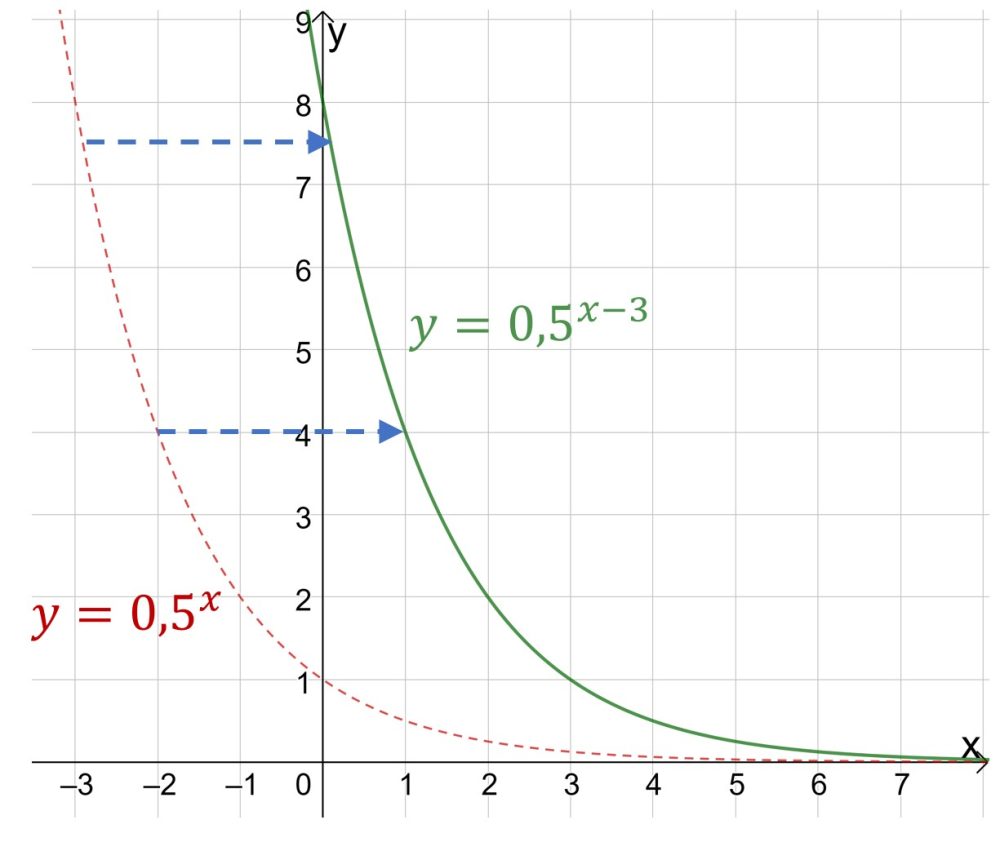
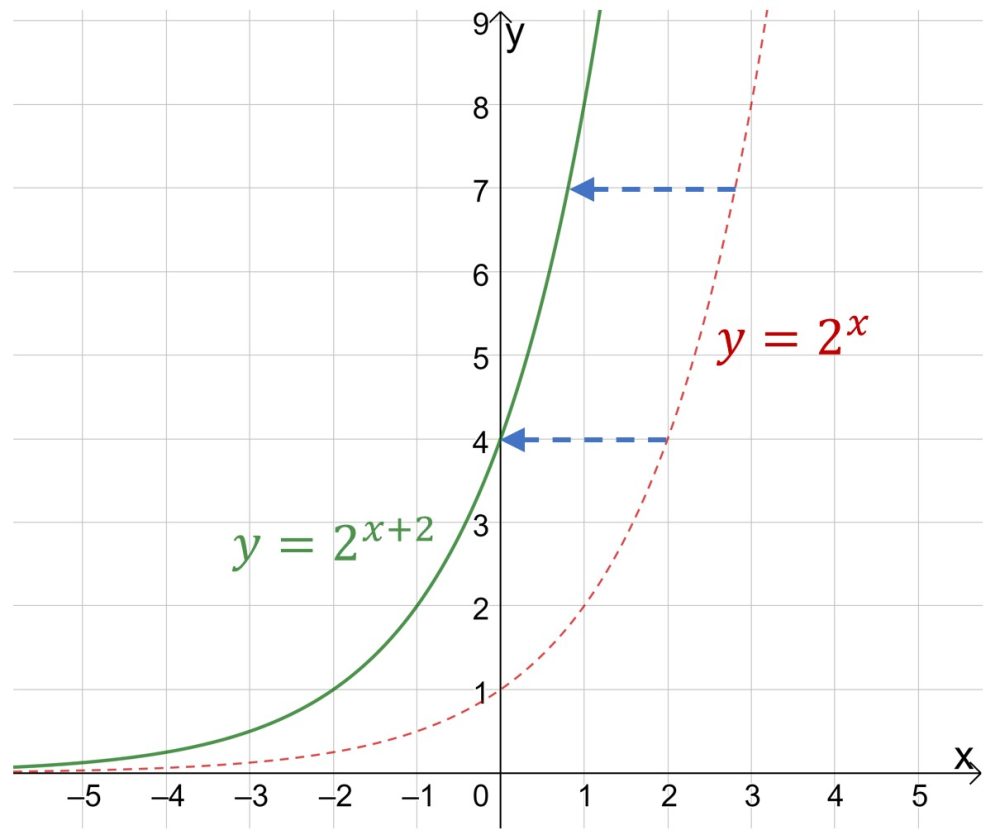
Если вдруг у Вас на экзамене все эти смещения туда-сюда вылетели их головы, то берите одну-две-три точки (по ситуации), подставляйте в уравнение функции и находите нужные Вам коэффициенты.
И хотелось бы напомнить , что основание логарифма и основание показательной функции МОГУТ БЫТЬ ТОЛЬКО ПОЛОЖИТЕЛЬНЫМИ.
8) Ну и нельзя оставить без внимания задания на нахождение точек максимума и минимума и на нахождение наибольшего и наименьшего значения функции. Тут советов будет несколько:
1) Повторите таблицу производных функций и вспомните формулы для производной частного и произведения.
2) Если Вам нужно найти наибольшее или наименьшее значение функции, содержащей логарифм, например 
, то в большинстве случаев это значение достигается при таком х, когда логарифм обращается в нуль, а число под логарифмом рано единице. В данном случае точка экстремума равна -4. Именно в этой точке достигается наименьшее значение функции.
3) Если Вы имеете дело с иррациональной функцией, например 
, то точка экстремума может быть найдена с помощью формулы для расчета вершины параболы. Одним словом, координата вершины параболы это и есть точка экстремума.
4) Теперь поговорим о показательных и логарифмических функциях. Если график возрастающий, то есть основание больше единицы, например 
, то экстремум (в данном случае минимум) достигается в вершине квадратичной функции 
. Ну а подставив точку минимума в саму функцию, Вы имеете все шансы быстро и легко найти наименьшее значение.
С логарифмической функцией дела обстоят аналогичным образом. Давайте рассмотрим функцию вида 
. Основание больше единицы и равно 5. Значит функция возрастающая. Смотрим внимательно на аргумент под логарифмом. Он представляет собой квадратичную функцию, графиком является парабола с ветвями вниз. Найдя вершину параболы по формуле xверш=-b/(2a), вы найдете точку экстремума, в данном случае максимума, ну а подставив ее в саму функцию, вы найдите ее наибольшее значение. И для полноты картины, предлагаю рассмотреть убывающую логарифмическую функцию 
с основанием меньше единицы и равным 1/3. Подлогарифмическое выражение также представляет собой параболу с ветвями вверх. Найдя вершину параболы, вы найдите точку минимума, а подставив ее в саму функцию, вы получите наибольшее значение функции.
PS: Наверное, многие задумались, почему, подставляя точки минимума, мы получаем наибольшее значение. Ответ прост – если Ваша функция убывающая, то чем больше аргумент, тем меньше значение самой функции.
9) В своей статье я совсем не затронула задачи на вероятность. Думаю, со вторым номером из кимов справляются практически все. А вот 10 номер такой непредсказуемый, столько интересных и новых задач. И каждая задача не похожа на предыдущую… Здесь сложно дать какой-либо совет. Проработайте задачи из открытого банка ФИПИ, с сайта Решу ЕГЭ, посмотрите свежие сборники 2022 года, варианты Статграда.
Я постаралась очень кратко пробежаться по основным ошибкам выпускников. Если Вам эта статья будет хоть на 0,01 процента будет полезна, то значит, писалась она не зря.
PS: Хотелось бы выразить благодарность Филину Арсению Андреевичу за ценные замечания и помощь в публикации. Он опытный преподаватель, выпускник Физфака МГУ, в прошлом призер олимпиад Физтех и Ломоносов.
Ну а если Вы хотите повторить все темы перед экзаменом, обобщить знания, проработать свои ошибки и узнать еще больше подводных камней, смело могу порекомендовать финальный курс по математике, который будет проводить сам Арсений. Старт 17 мая.
