Недавно ФИПИ опубликовал новые проекты КИМов ЕГЭ почти по всем предметам. После общественного обсуждения по этим вариантам, возможно, будут сдавать экзамен нынешние 10-классники.
Следует отметить, что, возможно, эта “перспективная модель” ещё очень сильно поменяется, прежде чем стать официальной демоверсией [так и случилось, см. ниже]. Так было, например, при внесении существенных изменений в формат ОГЭ: проект был очень страшным, но в итоговую демоверсию внесли не такие “жесткие” изменения.
Кстати, что изменения ОГЭ, что изменения ЕГЭ свалились на головы именно школьникам 2011 года поступления. Это связано, как я думаю, с введением новых федеральных стандартов – ФГОС. Так что изменения в ЕГЭ – 2022 были для меня вполне ожидаемы.
Основные изменения
В тестовой части ЕГЭ ликвидировали самые простые номера 1-3. Это простейшая текстовая задача, умение находить наименьшую/наибольшую точку на графике и простейшая геометрия как правило на знание формул площадей треугольника, прямоугольника и трапеции. А ещё почти все “старые” номера поменяли местами. Теперь вариант выглядит так:
Часть с кратким ответом:
Новый №1 — это №5 из нынешнего ЕГЭ, простое уравнение: показательное, логарифмическое или иррациональное.
Новый №2 — это “старый” №4, теория вероятностей.
Новый №3 — новое задание, на умение работать с графиком функции
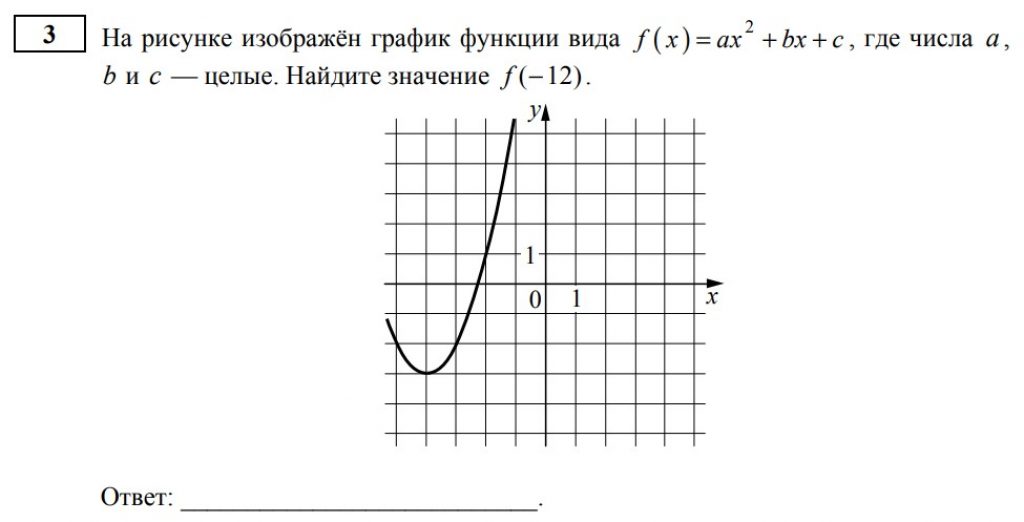
Новый №4 — это “старый” №6, простая задачка по планиметрии.
Новый №5 — это “старый” №9, пример для вычисления с тригонометрией, степенями или логарифмами.
Новый №6 — это “старый” №8, стереометрия.
Новый №7 — без изменений, на производную функции.
Новый №8 — это “старый” №10: вычисления по заранее известной формуле.
Новый №9 — это “старый” №11: сложная текстовая задача.
Новый №10 — опять теория вероятностей, но немного труднее чем №2.
Новый №11 — новое задание, на комплексные числа. Её условие приведём ниже.
Новый №12 — без изменений, нахождение экстремумов функции через производную.
Часть с развернутым ответом:
В 13-ой задаче убрали пункт б) – отбор корней уравнения, принадлежащих промежутку. Оценивается задача по-прежнему в 2 балла.
Задача №15 теперь состоит из трёх пунктов: нужно решить неравенство, уравнение и ещё их систему. Оценивается она теперь в 3 балла, раньше было 2 балла.
В остальном изменений почти нет. Разве что поменяли местами 16 и 17 задачи.
Комплексные числа
Одно из новшеств в “новом” ЕГЭ по математике – задача на комплексные числа. Вот так она выглядит:
Про комплексное число z известно, что |z-4-7ⅈ|=|z+4-ⅈ|. Найдите наименьшее значение |z|.
Решение задачи строится на использовании формулы для модуля комплексного числа 
: 
. Следует представить z в виде 
, воспользоваться формулой для модуля, упростить выражение, а затем изобразить решение уравнения на плоскости (a;b) – это будет прямая. Модуль числа z при этом будет иметь смысл рассояния до точки на прямой до начала координат. Наименьшим это расстояние будет в случае перпендикулярности отрезка от точки на прямой до начала координат к этой самой прямой.
Полное решение посмотреть можно тут:
Не стоит бояться необычных формулировок, требующих геометрических построений: рецепт здесь один — тренировки. Чем больше задач вы решите — тем легче вы сможете применять геометрические трюки в необычных ситуациях.
ВНИМАНИЕ! Выше рассмотрена ПЕРСПЕКТИВНАЯ МОДЕЛЬ, от которой все же решили отказаться. Опубликована официальная демоверсия, и она имеет мало общего с перспективной моделью, о которой мы говорили выше.
Огромное спасибо за статью! Было интересно узнать новости насчёт ЕГЭ-2022 по математике. Осталось только хорошо подготовиться и сдать 🙂